Moments and Torque

In our previous posts on statics, we looked at an introduction to terminology and static force systems.

Now let's move on to rotational force.

Whenever an object has a force applied to it at a point other than the center of gravity, it may start to rotate. The rotational tendency of an object is known as the object's moment.

The application of that force is known as torque.

In the case of the featured image at the top of this post, gravity exerted force on the pickup truck. The lift arms provided a reaction force in response to gravity. Unfortunately for the owner, the lift arms did not fully support the pickup truck.

Since gravity is a harsh mistress, disaster is inevitable.

Let's look at a very simplified thought experiment to consider how the truck broke in half.

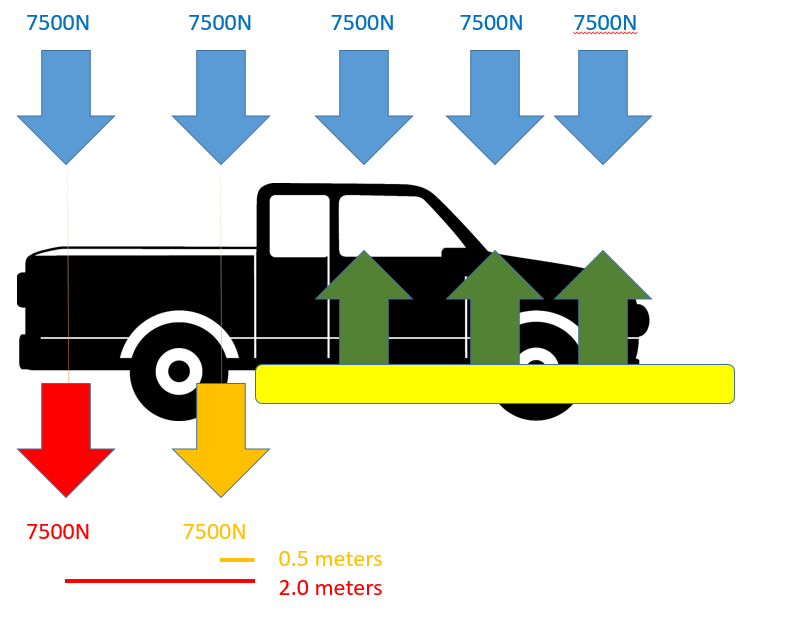
The pickup truck weighs in at around 8500 pounds. This works out to roughly 37,500 newtons. For the sake of the problem, I'm going to say that the truck has 5 roughly even discrete forces acting on it across the length of the truck. The back two forces are unsupported and occur at 0.5 meters and 2 meters from the edge of the lift arm. For the sake of argument, we'll say that one force is the wheel weight and one is the bed weight so that people don't email me saying that this isn't how you'd model that. Anyway!

We have a few equations we can use to solve this; however, they all lead to the same result.
||M|| = Fd

M = r x F (cross product, not multiplied by. You'd use this if you need a vector result)

||M|| = ||r|| ||F|| sin θ

M stands for Moment. This is our torque produced. Sometimes it is viewed as a vector, while other times, only the magnitude is considered.

F is our force applied, which is either a scalar or a vector.

d is our lever length.

θ is the offset angle from the force vector and the lever arm. Think of it as how you'd compensate mathematically for someone pushing on a lever at any angle except perpendicular.

r is the position vector as seen from our reference point to the point of application.
The direction of rotation uses the right-hand rule, as shown below.

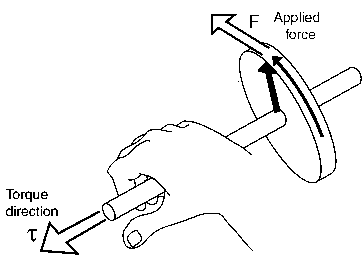
The right-hand rule for torque requires one to grasp the shaft with fingers curling in the direction of rotation. The applied torque, Ï„, occurs in the direction that your thumb is pointing.

With all this being said, the red 7,500N force was applied 2 meters from the support point.
M = 7500 * 2 = 15,000 Newton-meters of torque.

This causes 15,000Nm of torque to be applied because of that force. This can be compared to the 3750Nm of force due to the orange force. It's irrelevant, but if we view the axis of rotation as the plane formed by the edge of the lift arms, the torque direction is out of your screen towards your face.

Since the applied torque exceeded the yield strength of the chassis, we see a spectacular, catastrophic failure.

Check out our other articles on Introduction to Statics, Static Forces, and Force Couples.