Introduction to Statics

The study of mechanics can be divided into two major categories: statics and dynamics. Statics concerns itself with the equilibrium of bodies under forces without regard to time. Dynamics is the study of these bodies in motion.

To establish a baseline, let's look at a few basic terms and ideas before we dive in to the math in the next article:

Force:

This is best defined as one body acting upon another through one of several different methods. Objects can be physically moved by contact pressure, air pressure differences, electromagnetic wave propagation, or any number of other methods. Force is a vector quantity that typically causes movement in the direction where it is applied.

Mass:

Mass is the measure of a body's inertia. Inertia can be thought of as resistance to a change in motion. Mass is the amount of something that exists independent of the influence of gravity. Gravity is, instead, generally thought of as a function of mass. Mass is measured in kilograms.

Particle:

Particles are mathematical constructs that are best thought of as infinitely small points that have mass. This allows for easier calculations. Particles can be used where the dimensions of an object are irrelevant.

Rigid Body:

Rigid bodies are those where the change in distance between two points on the body under a given load is negligible when compared to the problem's constraints. If an axle bends by just a few microns over the range of no-load to full-load in a dump truck, it's probably not useful to include that information in your calculations. It is safe to assume that the axle, in this case, is rigid.

Space:

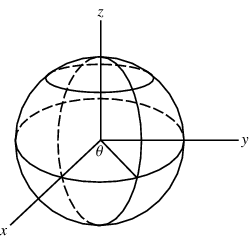
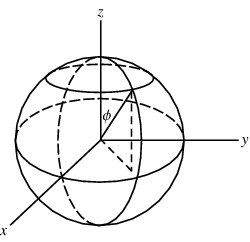
Space is the region in which we describe the position of bodies through coordinates and linear/angular measurements. In 2d space, an (x,y) or (r,θ) arrangement will suffice. In 3d space, an (x,y,z)[cartesian], (r,θ¸z) [cylindrical], or (r,θ¸Φ) [spherical] notation is required. Throughout all articles in this blog, the spherical coordinate system will assume θ means the inclination from the horizontal plane while Φ represents the inclination in the vertical plane.

Scalars vs Vectors

Scalar quantities are those that possess only magnitude. For example, you may be traveling 50 miles per hour. Your lightbulb may be using 60 watts of electrical energy. Your water may take up one cubic centimeter per gram.

Vector quantities are those that possess both magnitude and direction. You could be traveling 50 miles per hour in the southwest direction. Your canned lights in your house may be emitting 1000 lumens of light in the r direction where θ is less than zero and 0 lumens otherwise. If that didn't make sense, you might want to review using the spherical coordinate system.

Types of Vectors:

Free Vector: This type of vector is independent of the location it is applied. If I push a box from the bottom and the energy used and motion obtained is the same as if I pushed it from the top, my pushing may be modeled as a free vector. This requires the object to not undergo any rotation as a result of the vector force.

Sliding Vector: Sliding vectors are vectors where the vector is applied in the same direction and magnitude along a specific line of action. The actual point of application does not matter.

Fixed Vector: Fixed vectors have a specified magnitude, direction, and point of application.

Unit Vector: This is a specific type of vector where it represents only direction. This can be found by dividing a vector by the second norm of that same vector. The second norm can be found in the following equation:

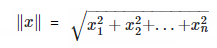
If my vector was u = <1,3,5>, ||u|| = √(1+9+25) = √35, then my unit vector would be <1/√35, 3/√35, 5/√35>.

Newton's Laws of Motion:

First Law: A particle remains at rest or continues to move with uniform velocity if the net force acting on that particle sums to zero.

Second Law: The acceleration of a particle is proportional to the sum of forces acting upon it. This is more traditionally known as Force = mass * acceleration.

Third Law: The forces of action and reaction between two bodies are equal in magnitude and opposite in direction.

Gravitation: When considering the weight of an object, we must consider the object's mass and the gravitational force acting on that object. This can be expressed by

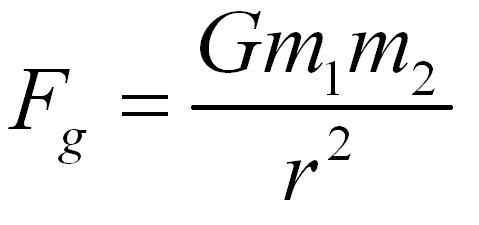
where F is the force of attraction between two particles, G is the gravitational constant ( 6.673*10^-11 m³ / kg s² ), m1 and m2 are the object masses, and r is the distance between the center of mass from one object to the center of mass of the other object.

For most purposes, this can be ignored as the influence of gravity on two adjacent objects is many, many orders of magnitude smaller than the impact of the gravity of the Earth.

This equation can be simplified when considering only items on the planet Earth by the equation W = mg where weight (W) in newtons (N) is the product of mass in kilograms (kg) multiplied by the acceleration due to gravity which is approximately 9.81 m/s².

Check out our next post on static forces in our continuation of Statics. After that, look into rotational force, then force couples.