What is Reactive Power?

In an earlier post, I went over some electrical power terminology. Recently someone asked about what a "KVAR" was, and I decided to write an article about it.

First, a KVAR means "kilovolt-ampere reactive" and is the conventional unit of measurement for reactive power.

A volt-ampere is the traditional term for the unit of measure of complex power.

The watt is the unit of measure for real (or true) power.

My previous post should explain the relationship between these.

As a quick note: If you already know the angle of impedance for the circuit and another measure of power, it's probably faster to use the trigonometric "power triangle" thumb rules in the previous article. This article assumes a complicated circuit where thumb rules are unusable.

Now that we have that out, I'll get to the long-awaited mathematical definition of reactive power. In this series of equations, we define reactive power as "Q."

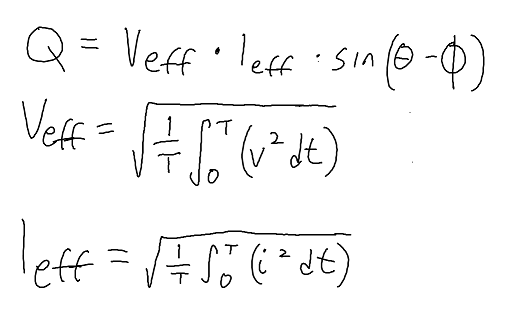
Q will be in units of the volt-ampere reactive. We get this by multiplying the effective voltage equation of a circuit by the effective current of a circuit by the sine of the voltage phase angle minus the current phase angle. This begs the question, "What is effective voltage and how do I calculate it?"

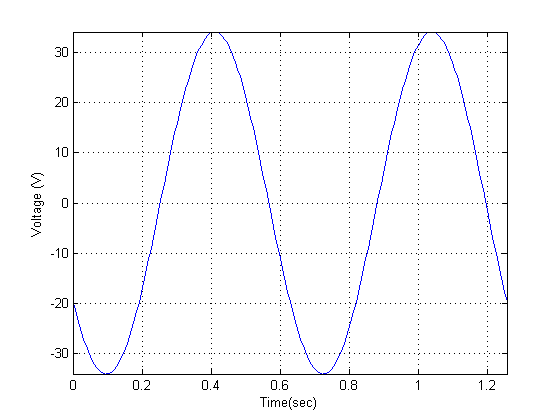
Consider a sine wave. It oscillates from, in this case, about -32 volts to +32 volts. If you averaged all of the values of our voltage across one full cycle, you'd get 0!

Obviously, that isn't a very good system.

Instead, we take the "root mean squared" value of the voltage. The most accurate way to do that is with the effective voltage and effective current equations I have posted.

In this case, T acts as your period for one full cycle of the sinusoid.

You take the integral of the equation that describes the square of your voltage from 0 to one full cycle, T. You then take the square root of that value.

A generic sine wave will have a RMS value of about 70.7% of the maximum amplitude of your function. That means our RMS voltage for the sine wave shown is about 23 volts.

Remember that you have to have already solved the equation that describes the voltage and current of the circuit or relevant component in both time domain and phasor notation. That's an entirely different lecture for later. Let's focus on this topic for now.

Why can't we use 70.7% for everything? What if you were calculating the RMS voltage for a square wave? Sawtooth wave? What if there's regular interference to account for?

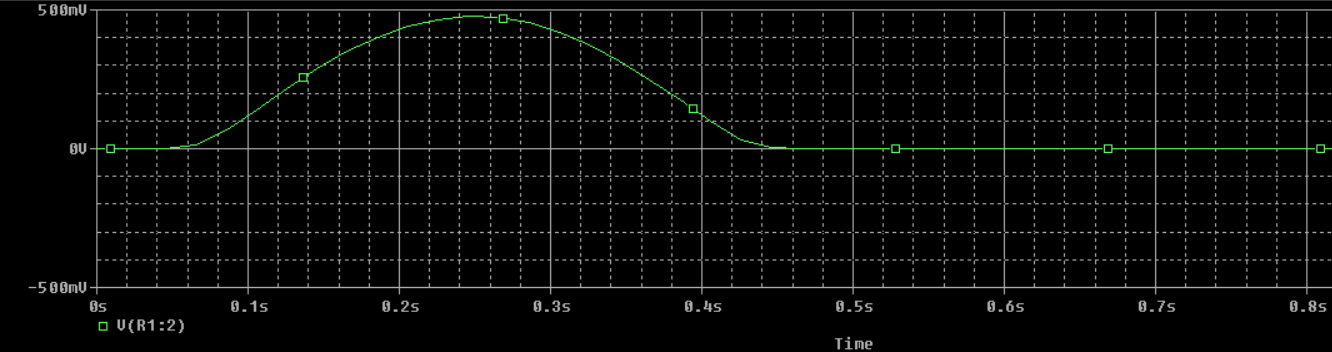
What if our sine wave looks like a rectified sinusoid shown above? That's where the need for calculus kicks in. As a quick warning: you can't just find the area under the curve using geometry tricks. The "squared" in "root mean squared" prevents that trick from working. We'll cover how to calculate the voltage and current equations in another article. To determine the theta and phi values for phase angles, check out my article on phasor notation conversion.