Analysis of 2-Phase Aspiration-Level and Utility Theory Approach to Large Scale Design

I. Summary of Research

Introduction and Background

In Callaghan and Lewis’s work on utility theory, the application of utility as it applies to the design of multiple major models of a proposed aircraft is explored [1]. This exploration involves the use of a case study involving both engineering and business students at the university level. This study found several fundamental facts regarding utility theory with regard to solution value quantization, preference profile assessment difficulties, and resultant scaling. Overall, this study has helped further elaborate on utility theory as applied to design.

In utility theory, it is necessary to use a formalized analysis method to select a design path from a series of alternatives. Alternatives are shown using mathematical constructs in terms of units called “utils.” These mathematical concepts are typically developed with attributes multiplied by weighting factors as in the Figure of Merit calculation shown by Thurston [2]. These utility functions allow a decision-maker to determine the design path with the most utility.

The Aspiration-level Interactive Method makes use of the identification of non-dominant options. Dominant options are those which meet all design criteria while excelling relative to other options in at least one design category. AIM methodology is considered a hybrid approach to utility theory-based design.

As it is critical to make engineering determinations as early in the design lifecycle as possible, it is necessary to eliminate uncertainty regarding decisions quickly when conceptualizing a design [3]. To reduce risk, utility theory may be used by decision-makers to ensure the most useful designs are approved for consumer use. This top-down design methodology considers design options contrasted against the preferences of each designer. Each major characteristic is weighted. Finally, the overall utility of each design is calculated in order to provide a true rank for each option set [1].

In the stage where designer preferences are modeled, it is critical to understand the stance the designer has on risk. Designers may be averse to risk, prone to taking risks, or neutron on the issue. This typically results in a situation where risk improves the performance of the design substantially past a certain breaking point if a successful product is created. However, less risky options tend to have higher utility most of the time as they have a higher probability of success. By understanding the stance of each designer, decision-makers can probably weigh each designer’s recommendations appropriately.

Methods

For their study, Callaghan and Lewis devised a method whereby both traditional Utility Theory and AIM theory could be combined into a single unified idea. As shown in Figure 1, this two-phase method makes use of the elaboration of alternatives with specified desirable attributes. These alternatives are scored based on their utility in order to create a list of dominating alternatives based on designer input. The design manager sets criteria on his or her own and applies this to the dominating alternatives to create a ranked list of the remaining alternatives [1].

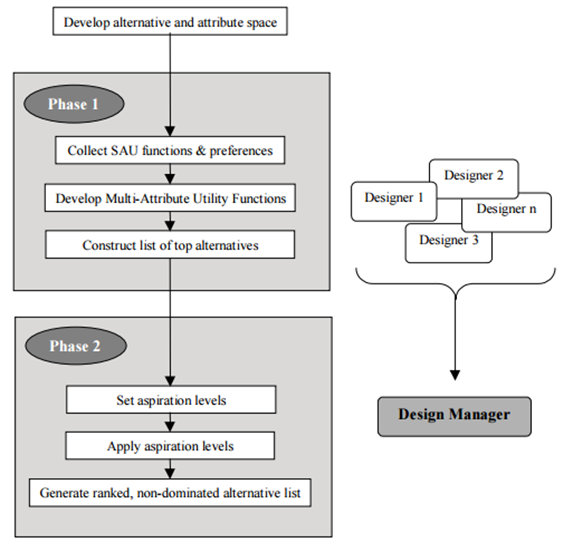
To test this using a real-world scenario, Callaghan and Lewis collaborated to create a design challenge whereby graduate-level engineering and business students would create an aircraft design. The airplane was to be outfitted based on minimizing cost, minimizing weight, maximizing passenger capacity, maximizing range, and maximizing speed. Table 1 shows the possible arrangement of design options provided to the students for selecting from.

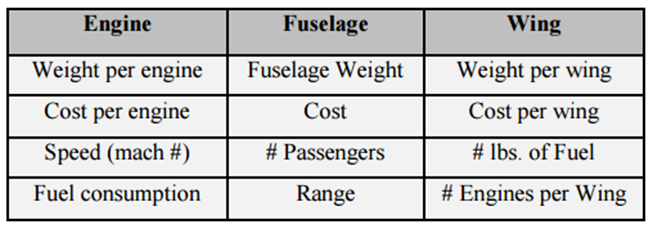
The students were provided with 5 different possible selections in three major categories to build the airplane. Table 2 discusses all possible technical specifications available to the design team. Using this data, the design teams were instructed to grade the relative importance of each major attribute.

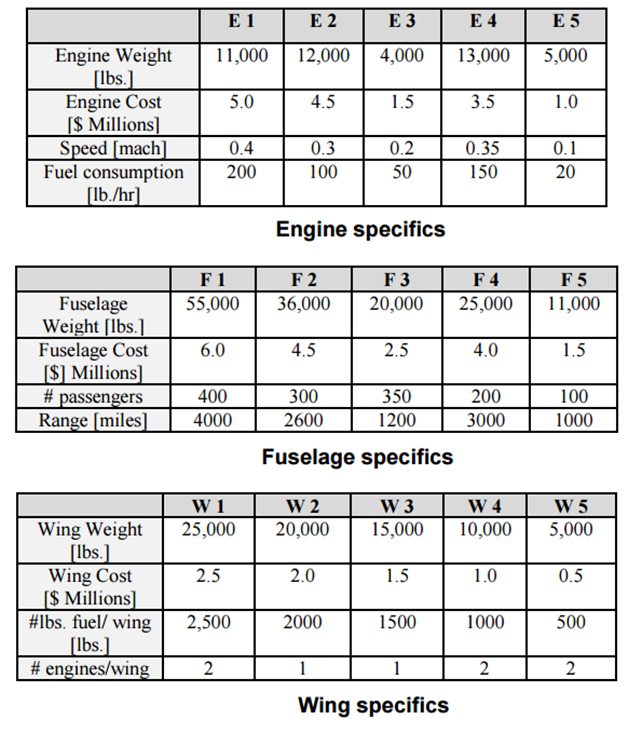
The attributes were graded with the results tabulated. The following results were seen as shown in Table 3. Divergent opinions were encouraged by mixing business majors with engineers. This was done to promote conflict in design criteria as business majors were expected to have a higher interest in return on investment while engineering majors were expected to be more interested in performance.

Results

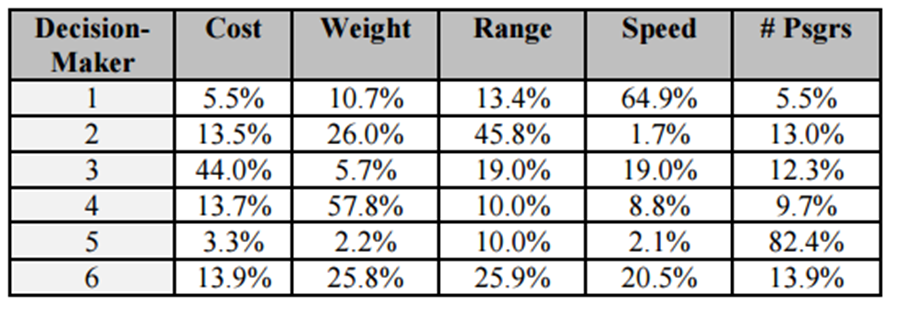
Table 4 discusses the final ranked design scores. By converting design criteria weights and scoring results for each attribute to a common unit, solutions could be accurately ranked. These ranked solutions are then provided to the top-level decision-maker for a final assessment.

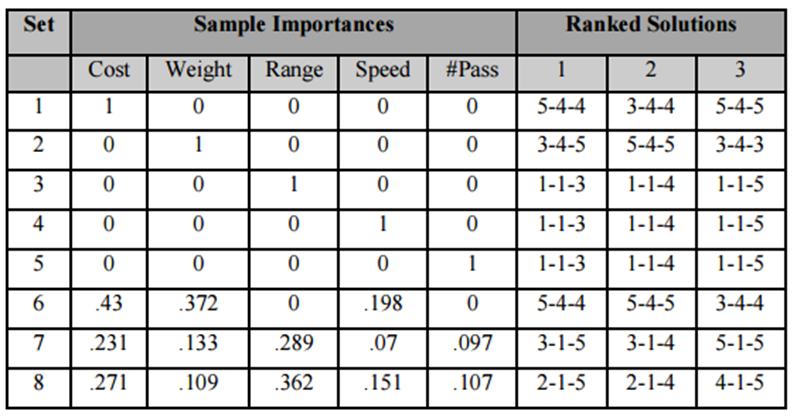
From a metrics perspective, different decision-makers provided substantially different design weighting. For example, a profit-oriented decision-maker would tend to favor passengers and cost over performance metrics. By allowing for multiple decision-making biases, the method discussed by Callaghan and Lewis allows top-level decision-makers to review recommendations with an understanding of the relative importance of each definable attribute from each subordinate decision-maker.

II. Discussion of the Paper

This paper shows merit in that it provides excellent insight into Utility Theory and AIM Methodology. By providing a full case study with an explanation of each milestone, Callaghan and Lewis break each step down so that an uninitiated designer can use this to perform their own decision process. By defining decision-makers as risk-averse, risk-neutral, and risk-prone, an important distinction is made with regard to how some individuals tend to bias their decisions.

Possibly the most insightful is the idea of attribute biasing. As seen in other design methodologies such as House of Quality [4][5], defining Utility Theory in terms of mathematical weights with universal units provides an excellent understanding of how the system works [1,2].

However, one relatively minor point of consideration is the incorrect classification of graphs in Figure 7 of Callaghan and Lewis’s paper. Lewis and Callaghan incorrectly refer to these graphs as holding a shape similar to an exponential function. However, only one curve in Figure 7 approximates an exponential function. The other curves are monotonic rising logarithmic curves which indicate risk-averse behavior. This may have been an error on the part of the authors as exponential graphs are the inverse of logarithmic graphs.

III. Future Possibilities

Based on the research conducted by Callaghan and Lewis, Utility Theory will see further use in other probabilistic modeling systems. Utility theory is already used in mathematical optimization techniques found in computer science. In the Requirements Problem solution methodology, requirements are similarly studied from a systems engineering perspective.

This method is novel in that it suggests adaptive systems which can alter their own characteristics based on run-time requirements. Real-time system response may allow for multiple design paths to be viable when designing a system [6]. For example, a laptop optimized for performance for one user state may automatically adjust power consumption for another user state. By doing this, multiple options in the design space are possible to be implemented simultaneously.

Another novel area of recent research in Utility Theory is in the scoring of attributes when the original importance of the attributes is not known [7]. This allows for group-based decision-making using fuzzy and number theory and entropy theory combined with utility theory. Although this field is still new, it shows great promise to allow for the interpolation of missing data in future cases.

References:

[1]       Callaghan, A. R., and Lewis, K. E., 2000, “A 2-phase Aspiration-Level and Utility Theory Approach to Large Scale Design,” Des. Eng. Tech. Conf., pp. 1–11.

[2]       Thurston, D. L., Carnahan, J. V., and Liu, T., 1994, “Optimization of design utility,” Am. Soc. Mech. Eng. Des. Eng. Div., 116, pp. 801–808.

[3]       Pahl, G., Beitz, W., Feldhusen, J., Grote, K., 2007, Engineering Design: A Systematic Approach, Springer, London.

[4]       Hauser, J. R., and Clausing, D., 1988, “The House of Quality,” Harv. Bus. Rev., pp. 63–73.

[5]       Olewnik, Andrew, Lewis, K., 2005, “Can a House Without a Foundation Support Design?,” IDETC/CIE, pp. 1–11.

[6]       Jureta, I., 2015, “Requirements Problem and Solution Concepts for Adaptive Systems Engineering, and their Relationship to Mathematical Optimisation, Decision Analysis, and Expected Utility Theory,” ARXIV [Online]. Available: http://arxiv.org/abs/1507.06260.

[7]       Zhang, F., and Xu, S., 2016, “Multiple Attribute Group Decision Making Method Based on Utility Theory Under Interval-Valued Intuitionistic Fuzzy Environment,” Gr. Decis. Negot., 25(6), pp. 1–15.