Anisotropic Image Filtering (Watercolor) Using Differential Equations

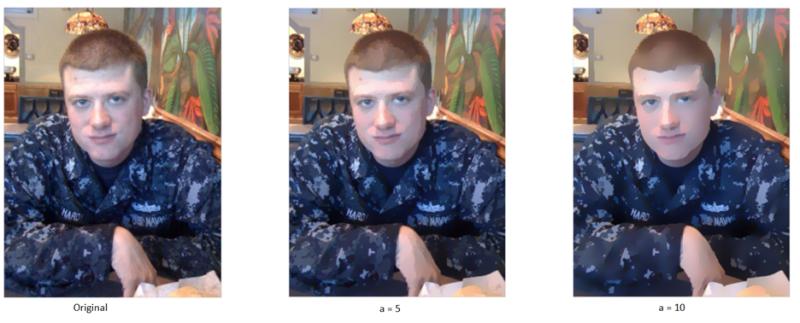
Let's look at converting a picture into a "comic book"-style image using math. This article assumes that you have some familiarity with calculus to get the most out of it though there's plenty of explanation if you're not familiar. I did not include the derivation of the PDE, sorry. Yes, this is more complicated than just dropping it into Midjourney, but you're learning the math under the hood!

Please note that you may have to resize your image as MATLAB has some trouble with larger images. Please also note this requires the Image Processing Toolbench which may be a premium feature depending on your license.

Anisotropic filtering makes use of a solution of the Heat Equation. The technique we'll use here also uses an edge-stop equation to preserve the edges of our image. Our function, heat, is called by a loop script so that the heat function is applied to all 3 color channels of the image. We pass both the input image and a weight factor, 'a,' to our function for it to process.

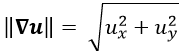
Our edge stop equation takes the discrete derivatives of the image in both the x and y-direction. It then computes the magnitude of the gradient of the image using the discrete directional derivates. Derivatives are used as they indicate areas where the rate of change of the image is high: edges. This is weighted (by a constant 'a') and then factored into our anisotropic equation.

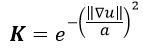
The anisotropic heat equation is a solution of the general Heat equation partial differential equation. If you think of an image as a three-dimensional field where pixel values from 0-255 are energy levels on a cartesian plane, it makes more sense. The anisotropic equation is iterated the number of times specified by the programmer.

Each iteration has a certain change value (our delta-time) specified by the programmer. Changing the deltaT value can result in instability in the equation and is not recommended. To visualize what is happening, think of a contour map of a mountain. As time passes, the mountain erodes into a smooth hill with a large base.

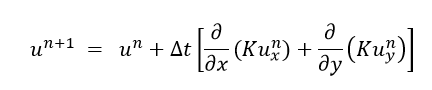
Similarly, a hot point on an object will cool, which will raise the temperature of the surrounding area. Using this concept, our anisotropic heat equation smooths a color channel by lowering the high pixel value areas. Our edge-stop equation prevents smoothing from crossing any area where the 2nd discrete derivative of the pixels is too high. The result is a watercolor effect that makes your input image look like a comic book.

Now that we've covered how it works let's have some code. If you want to use this, please link to this page and provide proper attribution per Creative Commons licensing rules. To run this in MATLAB, create a function named 'heat,' copy everything from the 3rd line on down, save it, then imread your test image into variable 'A' and kick everything off by pasting the for loop into the command line.

Good luck!

% *******Enter this at the command line ***********
A = imread('testimg.jpg'); % Your image name here
for i=1:3;
B(:,:,i) = heat(A(:,:,i),10);
end;
imshow(B)
% ************ Create This Function ***************
function [u] = heat (f,a)
% Anisotropic heat equation
% Author: Tyler Hardy
% Contact: www.wirebiters.com %
Input: Initial image
%Output: Solution of the heat equation u
%Parameters
dt = 0.1; %Time step
T = 20; %Stopping time %Initialize u=f. Convert to double so we can do arithmetic.
u = double(f);
[m,n] = size(u);
for t = 0:dt:T % begin for loop *********
u_x = (u(:,[2:n,n]) - u); % first x derivative
u_y = (u([2:m,m],:) - u); % first y derivative
magnitude = sqrt(u_x.^2 + u_y.^2); %magnitude
K = exp(-(magnitude/a).^2); % K calculation
P_x = K.*u_x; % heat equation step1
P_y = K.*u_y; % heat equation step1
D_px = P_x - P_x(:,[1,1:n-1]); % heat equation step2
D_py = P_y - P_y([1,1:m-1],:); % heat equation step2
u = u + dt * (D_px + D_py); % heat equation step3
imshow(uint8(u));
title(['t=',num2str(t)]);
drawnow; % This command is used for iterative drawing in MATLAB
end % end for loop ******************
u = uint8(u);
end % end function